Glitter text
I have glitter text! I made it myself in SVG. And I can make you one too.
What is glitter?
It’s little reflective pieces of something. I checked on Wikipedia, and supposedly it achieves its look by having multiple layers, “combining plastic, coloring, and reflective material.” (I couldn’t follow through to the source it cited though.) When you put glitter on a surface, the pieces get spread out at slightly different positions, so they reflect light at slightly different angles. Then when you either (i) look at the surface from different positions, (ii) wave it around, or (iii) light it from different positions, different parts of it light up, making a shimmering effect.
What should we build?
We won’t diverge too much from existing glitter text makers, which give you images like this:
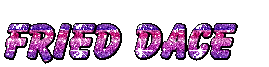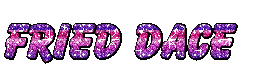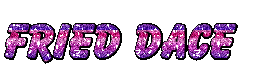
An image made by a site that was easy to find. They didn’t say I had to link back to the site, but I archived the search results page that I got there from.
Here’s what I notice about the example which we’ll try to replicate in our implementation.
- There’s a piece of text that’s filled with an animated glitter texture.
- It has a solid outline.
- The text itself doesn’t move around.
Let’s make an animated glitter texture and fill some text with it.
We’d infer from the text not moving that the shimmering must come from changes in light position. Although we won’t worry much about making something physically accurate, let’s think a little about how light makes glitter look the way it does, so that we can capture the key points in our texture.
A brief look at lighting
Let’s look at how light works in one particularly simple way of doing computer graphics. We’ll focus on the very basics because glitter will still look like glitter even if it doesn’t follow a realistic model.
The Phong reflection model defines a way to simulate how a point on a surface in a scene will look given:
- The “normal”—which way it’s facing
- The “view” angle—where you’re looking at it from
- The “light” angle—where the light source illuminating it is
- A few parameters about the object’s material, setting which is more of an art when you’re like me and you don’t actually have a real-life copy of the thing you’re rendering
Or so to speak. There are proper lectures on this, but I’m just writing down a rough summary in case you don’t want to go looking for good materials on the subject.
In this model, you get the result by adding up the contributions from three effects:
- “Diffuse” reflection—which makes a surface brighter when it’s facing the light source and dimmer when it’s facing away from the light source. I should clarify: the genius of Phong’s work isn’t figuring out that this is how light behaves. It was choosing which effects to combine and devising efficient ways to approximate them.
- “Specular” reflection—which makes bright spots where the surface could bounce light from the light source into the camera.
- “Ambient” lighting—which is a flat brightening to make up for any indirect lighting not included in this model.
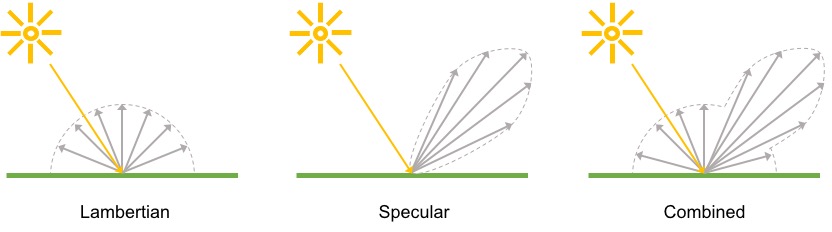
I always see the diffuse and specular reflections illustrated this way, so you might as well see it too. You’d never guess where I found this picture though. Apparently, TensorFlow has a Phong reflectance module. Follow the link for a copy of the license too.
There are a lot of scenarios where this model doesn’t look right, but it’s pretty convincing on glossy materials like plastic and metal. Wait, what did they say glitter was made out of? “Plastic, coloring, and reflective material.” Nice.
After a bunch of math, this model could tell you exactly which pieces of glitter will light up and when, given each piece’s angle and a detailed itinerary of where the light source will be at what time. We won’t need all that precision though. It only needs to look vaguely reminiscent of the real thing. I think we can get away with a few qualitative things from this model:
- The pieces are facing every which way, so the light source can’t be directly in front of all of them at the same time. Thus not all pieces will have the full diffuse reflection going. The pieces will sort of take turns being dimmed as the light source moves around.
- We won’t dim the pieces all the way to black, because there’s indirect light, which the model accounts for with the ambient lighting.
- Some pieces are lined up to reflect from a point on the light source’s path into the camera. Those pieces will briefly become very bright as the light source moves through those points, from the specular reflection. These will also sort of take turns.
How can we embed it?
These animations are meant to be used on web pages. We should build them on web technologies, and we should build them in a way that’s convenient to embed.
In the above sample from an existing glitter text maker, they gave me a GIF image. These are limited to indexed color, but supposedly there are ways to use more different palettes to get more colors. 256 colors are plenty for a single color of glitter, but you won’t convince me to stick to a single color of glitter.
For something like glitter, I suspect it wouldn’t compress well. The light changes slightly on each frame, which would affect all the glitter pixels. And although each frame is only a little change in lighting from the previous frame, any one frame would look totally random, which is the hardest to compress.
There’s an extension to the PNG format that adds animation, called APNG. I didn’t even notice that it was supported in so many browsers—93%, according to Can I use. I had always thought it was some fringe format, but apparently, Chrome added it in 2017, and there went the neighborhood.
PNG and APNG let you have semi-transparent pixels which GIF doesn’t, so this format would additionally let us have smooth edges when we use a transparent background. I think it still wouldn’t compress well though.
There are even newer GIF replacements than that, notably WebP and AVIF. WebP has wider browser support right now; AVIF supposedly has better compression (although I bet it was tested on sensible photos of things other than glitter).
The big draw for these in the context of being GIF replacements is their lossy compression, which was something you didn’t have for animated images back when you were choosing among JPEG, PNG, and GIF. But lossy compression has historically not done well with lots of random-ish detail, which is an important part of glitter’s look.
And then there’s outright video (I don’t know what exact formats are hot
right now).
It’s a step away from the embedding convenience of images.
You have to use a different HTML tag, <video>, to put it on a webpage.
If you want to use glitter text on someone else’s site, such as in a social
media post, using a video might be less flexible.
For example, they might keep videos separate from text, or they might require
viewers to click a video before it plays.
The video formats we see online also use lossy compression. The previous whining about lossy compression is pure speculation. I haven’t tried them out. This time, there are published examples of video compression doing a bad job on scenes with many particles, even one specifically about glitter.
Next are sort of the big guns for procedural graphics on the web—canvas, either with the generically named 2D context or with WebGL. You have to program these in JavaScript, which gives you lots of expressiveness. However, you can count on nobody letting you run custom JavaScript on their sites, so you should give up hope on being able to embed these canvas programs anywhere but your own site. That makes it a lot worse in embedding convenience.
These also take more processing power, which is the nature of procedural graphics.
I ended up most interested in using SVG. SVG is the kind-of-scary, barely-an-image-format format known for making little navigation icons that people can zoom in on without getting a pixelated mess. After all, that’s the first thing people do when they visit a site; they zoom in on the navigation icons. It seems SVG is less known as what I’m using it for here, a language for declarative procedural graphics.
You can write SVG in a restricted way with no JavaScript and no external
resources, which lets them work in good old <img> tags.
That’s pretty good for embedding convenience, although for posting on sites
other than your own, some sites are choosy about what image formats they allow.
The sites that are choosy usually don’t allow SVG.
The usual reason is that they’ll run all images through a resizing and
compressing pipeline built for raster images.
GitHub and Discourse allow it though, so I’m happy.
Oh, and you can bet your sweet bippy that animated SVGs take a lot of processing power. Declarative programming is a neat paradigm, but it ain’t magic.
Inside SVG’s figurative toolbox
This project gives us a few problems to solve.
First, we specify what pieces of glitter are where in the image and what direction each piece is facing. Second, we compute some kind of information about the lighting and how it changes over time as the light source moves around. Third, we use the lighting information to combine the glitter color and light color into a final color.
Let’s go through what solutions SVG has for each of these problems.
Laying out the pieces
What this means for a 2D graphics environment is to create an image of the pieces, with each piece colored based on its normal. We don’t need to settle on the association between color and normal for now, and we can later choose whatever makes the other problems easier. Here are three ways to create that image.
Obviously, there’s the vector graphics of Scalable Vector Graphics. You would write out all the coordinates of all the shapes you want and specify each one’s fill color. I think this approach would be kind of expensive though. The existing glitter text makers look like they treat each pixel as a different piece. I’d like to follow their lead in that. With this solution, we’d be losing big by having to store a bunch of coordinates and incur who-knows-what other overhead for each piece, when they’re so formulaically laid out. It might be a good option for coarser glitter though.
SVG can also embed raster images. Compared to vector graphics, this is much more efficient at representing a regular grid of independently sampled colors. It’s worse if we later do want to try coarser glitter though. You’re kind of stuck with making it so that one element from this grid controls one screen pixel. That’s because there’s no precise control over how it draws out this grid of colors. You usually get a blurry-looking thing rather than a grid of crisp squares.
And then there are filters.
These are built with a graph of filter “primitives,” most of which take in one
or more images and change them or combine them in some way.
Thus the overall filter defines some way to compute an image given an input
image.
It feels like a weird dream where shaders were designed by the people who
invented XML.
And where half of the operations are from a 90’s version of Photoshop and the
other half are from a linear algebra textbook.
Anyway, a few filter primitives don’t take in an input image, and you can use
them as a starting point when you don’t already have an image to start with.
Other than one that embeds a raster image and one that fills the canvas with a
solid color, there’s feTurbulence, which generates Perlin noise.
Noise is, broadly, what we want: a concise instruction to fill in a bunch of
pixels randomly.
However, Perlin noise, specifically, is designed to produce a smooth, spatially
continuous texture.
That’s not what we want for this project.
We’d prefer to have discontinuities: solid shapes for the pieces of glitter
with instantaneous changes for the edges between them.
In addition to these techniques for drawing the normals, you can make a smaller rectangle of texture as a pattern and tell the renderer to repeat that across the canvas. Using a pattern is less prestigious in case people notice it being repetitive, but it would save data for the vector graphics and raster images options by delivering only the smaller rectangle’s worth of random stuff.
Computing the lighting
In this step, we’ll do most of the math described in the lighting model, optionally with some simplifications. We’ll use the normals from the previous step as one of the inputs to the model.
SVG actually gives us a 3D lighting engine with feDiffuseLighting and
feSpecularLighting.
(Side note: the specular one uses the Blinn-Phong reflection model, the variant
with the half-angle thing.)
Unfortunately, it assumes a continuous surface, which makes it look weird when
the input has a bunch of small pieces with discontinuities in between.
It’s also kind of expensive for some reason, such that it either gets a lower
frame rate or uses more battery if the device can still keep up.
Maybe it’s implemented in software on my browser.
If we wanted to compute it ourselves, we probably could, albeit awkwardly.
feColorMatrix can perform affine combinations of channels,
feComponentTransfer’s type="table" can apply a piecewise-linear
approximation of unary nonlinearities, and feBlend can do some other basic
mathematical operations.
Again, it’s a bizarre way to write a fragment shader.
I doubt that a big stack of these would be any less expensive than the native
lighting filter primitives though.
There’s cheaper, of course.
One idea from that end of the spectrum is to use color cycling, which we
can do with feComponentTransfer supporting a discrete mode for applying
arbitrary, even animated palettes.
We’d have 256 possible pieces of glitter—enough to look fine when spread out
randomly IMO—and we’d cycle through lighting effects precomputed at times
throughout the light source’s movement.
For something in between, we could sample an animated texture with
feDisplacementMap.
This would give us access to more colors at any one time, up to 256 * 256
colors.
The separation of x and y sample coordinates might make some bookkeeping
easier.
There’s also plenty of flexibility in how we animate the sampled texture.
Applying the lighting to an object’s color
One of the few parameters in the Phong reflection model is a set of numbers describing what the object does to light at different wavelengths. That is to say, it’s the object’s color. (Other reference materials on the model expanded this to have separate sets numbers for diffuse, specular, and ambient. But we don’t need that extra fiddliness in this project.) Of course, it’s all math, and the color numbers are just another input in the formula. But it’s useful to think of combining the lighting information with the object color as a separate step, which would let us combine an image of different glitter colors with a relatively smaller number of lighting effects, the latter of which is indeed limited in some of the above computation solutions.
The formula in the model itself calls for the color to be (i) multiplied by a
diffuse and specular factor and then (ii) added to a specular term.
SVG can do that, using the feComposite filter primitive under various
configurations of operator="arithmetic".
We don’t have to follow the model exactly though.
As I mentioned before, I think there only needs to be some dimming and some
brightening.
There are some blend modes like hard-light that let you do both so that we
can use a single filter primitive, in case that has less overhead.
Solutions used in my version
To lay out the pieces: filters.
I use feTurbulence with a pretty high baseFrequency.
We would like to have an independent sample at each pixel, so a base frequency
of 1 would be tempting.
But the way Perlin noise generates a grid of gradients and comes up with a
smooth function following it, sampling that function at a frequency of 1 gives
exactly zero every time.
For a bunch of not-quite-scientific reasons, I’m using one over the golden
ratio.
Perlin noise (one octave, monochrome) at different frequencies. Frequencies f from left to right: 1, 0.99, 0.9, 1/φ≈0.618, and 0.5. f=1 is all gray but may be visible on high DPI displays. f=0.99 looks good in the middle but turns gray at the corners where sampling approaches integer coordinates. f=0.9 exhibits similar gray spots in a smaller 10x10 pixel pattern. f=1/φ (used in my version) looks alright IMO. f=0.5 and below start looking chunkier.
The result looks nice and noisy, with very little file size footprint.
There are a few things not entirely satisfactory about this though.
First, the image won’t scale right.
At higher resolution, in case of zooming or high DPI displays, there’s smooth
interpolation instead of crisp edges between the logical-pixel-sized pieces.
Second, SVG’s specification of feTurbulence calls for a random alpha channel
as well.
Popular implementations’ use of premultiplied alpha throughout rendering
results in the R, G, and B channels having lower precision.
Thus for now a browser would do all the work to generate four channels of
texture, but we’d get the best results by using only one.
Third, the generated values follow some kind of center-heavy distribution.
This could make it more complicated to get the distribution of normals we want
if we only know how to get there from a uniform distribution.
To compute the lighting: color cycling. It costs more in terms of file size to store the tables, but it was much faster in my experiments.
To recap, the reflection model I’m using has inputs for the normal, the “view” angle, the “light” angle, and the material parameters. Within this solution, we’ll animate across palettes for different values for the light angle. Within the palette, we get to choose 256 settings of the other inputs—normal, view angle, and material parameters.
In my version, I treat the camera and light source as far away from the glitter, so that the view angle and light angle are constant throughout the image. We’ll be composing the lighting information with the glitter color in a separate step, so we won’t need to eat up our palette entries with different glitter colors either. The rest of the material parameters I also hold constant in my version. All that remains varying is the normal, so we can choose 256 different normals.
I did some calculus to come up with a formula that would uniformly spiral around the front-facing hemisphere.

The 256 normals chosen this way. Left: colored by normal. Right: colored by index, from red (index 0) through orange (index 128) to yellow (index 255), with a gray line connecting sequential elements.
For symmetry, I made it have two opposing spirals coming out from the center, diverging from index 128. So with the non-uniform center-heavy distribution from the previous step, there will be more pieces facing forward toward the camera. I don’t know what the distribution of normals in real-world glitter is though, so whatever. At least our distribution won’t be lopsided.
This pattern causes another of the problems with my version. Because of the spiral arrangement of the indices, interpolating colors in the indexed normals image leads to a very un-smooth transition in the lit image. This makes the glitter look finer on high DPI displays, so much so that the animation is hard to see.
With the palette of normals, we can compute whatever lighting information we
want for each normal, for the fixed uniform view angle and material properties
(other than color), and for each of several light angles.
We put those values into an animated feFuncR/G/B/A with
type="discrete", and the renderer can go through them without doing any more
calculations at runtime.
Because we have this pre-baked lighting information, we can support multiple light sources at no additional cost at runtime. All we’d do is add up the diffuse and specular reflections from each light beforehand.
To apply the lighting to the glitter color: alpha-composite with white and black. The renderer I was experimenting on was noticeably faster doing a single blend operation than doing two for other solutions.

Applications of lighting information to a material color (red) showing diffuse reflection (varies vertically) and specular reflection (varies horizontally). Left: multiply by diffuse and add specular, as in the Phong model. Right: hard light of specular minus complement diffuse (used in my version).
In this solution, the shadow-ness from lack of diffuse reflection fights with
highlight-ness from specular reflection.
They cancel each other out until there’s only one left.
Then if the shadow wins, what’s left is applied as an opacity of black
alpha-composited with the material color, and if highlight wins, what’s left is
applied as an opacity of white alpha-composited with the material color.
Blending with black or white is the same as multiply or screen, so this is kind
of like the hard-light blend mode.
I’ve gone with this cheaper solution that is less accurate to the model, but the inaccuracy also increases the result’s saturation in a pleasing way. In places with lower diffuse reflection (black) would be added to specular reflection (white), e.g. in the bottom center of the sample images above, the Phong reflection model gives gray. The black and white alpha compositing, on the other hand, instead gives the material color.
The very bottom center, showing a hypothetical combination of no diffuse reflection and maximum specular reflection, is pretty far off, but I don’t think that’s geometrically possible.
Here’s how those normals look with the lighting information applied this way:
The normals again, this time lit by two orbiting lights, applied with alpha compositing to red material.
It actually looks pretty round and shiny now.
Additional experiments
We could, of course, use this technique to light something other than a random sheet of glitter. Here’s a normal map of a suitable “something” that I found online:

We can convert this to indexed color so that the normals get clamped to the ones we’ve precomputed the lighting for.

Here’s a different visualization of that, colored by palette index instead of by normal:

Then we can compute the lighting and apply it to a material color.
The effect of only having a discrete set of normals is that the curved surfaces look kind of polygonal, and they look as if they’ve been flat shaded. It’s kind of wild seeing non-triangular faces though.
Dithering can help make the image look more detailed. It was useful when computers only had 256 colors, and it’s useful here when we only have 256 normals.
The last mile to glitter text
The normals, colored by index:
Continuity error disclosure: with the pieces of glitter mostly forward-facing, the two-orbiting-lights pattern turned out to be too throbbing. In the rest of the project, I use a single light that circles around the camera.
The precomputed lighting effects:
The glitter colors:
Lit and applied: (animation suppressed 😵)
Masked by text shape:
Outline:
Drop shadow:
Filesize study
We gave filesize great consideration early on in choosing how to build this.
The “Look,” sample at the top of this article is 25,344 bytes gzipped.
I tried gzipping (-n) various prefixes of the sample to see how much each
part impacts the compressed size.
misc, 1,056 bytes, is the SVG code that doesn’t fit into other categories. Oh, and some gzip overhead.
font, 16,902 bytes, is a base64-encoded WOFF file. In binary, the font is 16,744 bytes, and it’s pretty high entropy. It’s good that it’s not much bigger through the base64 and gzip process. Maybe if we were smarter about this we could strip out any unused characters.
r, 399 bytes, is a table of 16 * 256 numbers, plus another copy of that
first row of 256.
This along with g, b, and a represent the color and alpha of the animated
palette for lighting.
We’re either acting as a shadow r = g = b = 0 or a highlight r = g = b = 1,
so the only numbers are 0 and 1.
Naively, you’d be able to express this data for the r component in 512 bytes.
There are lots of runs though, and it ends up a little compressed.
g, 251 bytes, and b, 244 bytes, are exact copies of r because we used white light. It’s lame that they take more space. There might be a different configuration that lets them compress better, but we don’t normally get to fiddle with these parameters on web servers.
a, 6,487 bytes, has the same 16 * 256 + 256 structure as r, g, and b, but the alpha channel takes on many different values. We should only need 256 possible values assuming an 8-bit alpha channel, so you could naively express this data in 4,096 bytes. But I’ve encoded these with three digits, which is more precise than necessary, and it indeed takes more space than 4,096 bytes.
text, 5 bytes, has three copies of the text, for the fill, outline, and
drop shadow.
These copies together take 5 bytes for a 5-character piece of text Look,,
which seems like a pretty good deal.
Effects not modeled
With this relatively simple model, we miss out on some effects.
Diffraction. Some glitter uses materials that separate light into different wavelengths so that it shimmers in a range of colors. YouTube records indicate that this kind of glitter was very popular in 2016.
We could maybe animate these colors into the lighting palette, but there’d be much greater pressure on the number of palette entries. Whereas for reflective glitter we only encoded normal direction into the palette index, these variants will need more. First, the separation happens in a specific direction, so the BRDF is anisotropic, and we’ll need to vary the palette entries in tangent/binormal as well. Second, the prized rainbow effect depends on the differences in light angle and view angle across the surface, so we’d prefer not to approximate those as uniform throughout the image. But as for the normals, we might be able to get away with fewer. I found that in some settings, particularly with holographic glitter, people actually like having the pieces as front-facing as possible, rather than at random. It turns out that the foremost experts on glitter are nail art enthusiasts, and practitioners have developed a “burnishing” technique to make sure the pieces are lined up flat. So we could have fewer normals, but we’ll also need multiple tangent/binormal and multiple view/light angles. If 256 combinations end up too sparse we could switch over to a different way to compute the lighting information.
For colored lighting effects, alpha compositing and hard light wouldn’t do a good job of combining the highlights with the material color. It might be better to go with the separate blending steps for shadows and for highlights.
Besides the performance hit from the more expensive computation and the extra blending, I also have a sneaking suspicion that rainbow-colored shimmering is less versatile from a graphical design standpoint.
Bloom. Supposedly really bright spots would have their light appear to bleed out into other pixels when you look at them through a camera. On computer screens, we can only show up to “255” brightness which any ol’ word processor is blaring all the time. Simulating this bleeding helps convey how bright a point is. You could probably add this on by convolving the bright spots with whatever kernel.
Doing it this way is computationally expensive though. I tried it briefly, and it took 6-7 percentage points more CPU on my setup. The effects used in the existing sample take 14-15% CPU. Maybe it’s something to consider in several years.
My last post was about either Default branches at work or How to keep the corners of clothing tags nice and sharp. Find out which.